Formulating a hydroponic nutrient solution – Part II: Micro nutrients
Micro nutrients are just as important as macro nutrients. Many growers fail to have their water analysed for all elements, and in some area one might have enough of a micro element in the water. By adding more with fertilizers, toxicity levels may be reached which can reduce yields significantly. The following example will use a sample water analysis to formulate the micro nutrient fertilizer requirements as according to the micro nutrient analysis in table below.
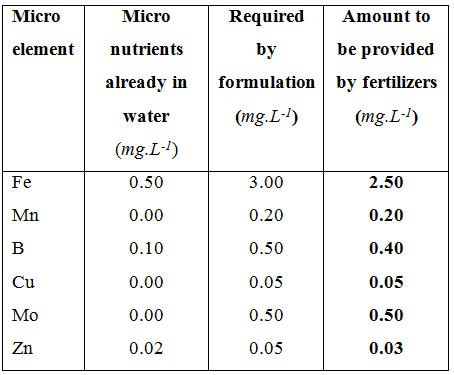
A list of micro elements that have to be provided by fertilizers of which part of the requirements are already present in the water.
The fertilizers that will be used in this example are listed in below. The percentages of each relevant micro element are provided in the last column.
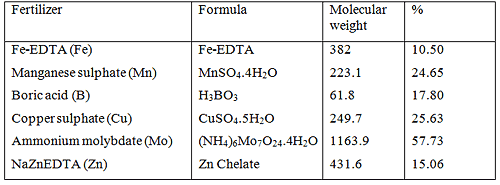
Fertilizers containing micro nutrients with their corresponding formulas, molecular weights and percentages of each micro element in the fertilizer
Solving for the micro elements is much easier than macro elements since each fertilizer contains only one micro nutrient. There is no sequence or algorithm to follow to determine the amounts of fertilizers to be used. The first micro element is iron (Fe). Iron is always applied as a chelate otherwise it is not absorbed by the plant in high enough quantities for normal growth. The iron chelate used in this example is NaFeEDTA, however, there are three other types that can also be used. Their selection will however depend on the water quality and pH. The iron content in NaFeEDTA is 10.5 %, the required concentration is 3.0 mg.L-1. The water analysis shows that there is 0.5 mg.L-1 Fe in the water. However, this Fe is not chelated and if the pH of the water is above 7.0, the iron uptake will be depressed. So, the water analysis in this case will be ignored for Fe (not for the other elements however). The following method will be used to determine the amount of NaFeEDTA to be added to 1,000 L of water in order to achieve 3.0 mg.L-1 Fe.
NaFeEDTA has 10.5 % Fe.
The following formula should be used.
![]()
where the following applies
C1 = Concentration of known element
C2 = Concentration of known fertilizer
C’1 = Concentration of required element
C’2 = Concentration of unknown fertilizer
![]() = The sign means “equal in proportion” or ratio
= The sign means “equal in proportion” or ratio
The following values will be replaced in the formula:
C1 = 10.5 mg.L-1 Fe
C2 = 100 mg.L-1 NaFeEDTA
C’1 = 0.3 mg.L-1 Fe
C’2 = X (concentration of NaFeEDTA in solution)
By replacing all the values we have the following
![]()
We need to solve for C’2:
![]()
![]()
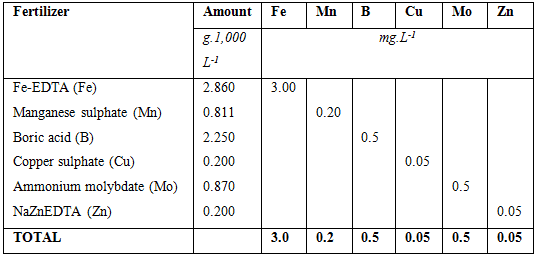
Thus in order to have a concentration of 0.30 mg.L-1 Fe in the solution, we need to add 2.86 g of NaFeEDTA in 1,000 litre of water.
Thus in order to have a concentration of 0.20 mg.L-1 Mn in the solution, we need to add 0.811 g of MnSO4.4H2O in 1,000 litre of water.
H3BO3: 17.80 % B
According to the water analysis there is 0.1 mg.L-1 B in the irrigation water so the amount of B required from fertilizers is 0.4 mg.L-1. The amount of Boric acid to add in the irrigation water (in a 1,000 L tank) will be:
The above procedure can be simplified using the following formula. It is actually the second last step in above procedure:
![]()
![]()
![]()
Now calculate the Manganese (Mn) required.
We will be using ![]() as Mn fertilizer. According to the water analysis there is no Mn in the irrigation water so the amount of Mn required from fertilizers is 0.2 mg.L-1. The amount of manganese sulphate to add in the irrigation water (in a 1,000 L tank) will be:
as Mn fertilizer. According to the water analysis there is no Mn in the irrigation water so the amount of Mn required from fertilizers is 0.2 mg.L-1. The amount of manganese sulphate to add in the irrigation water (in a 1,000 L tank) will be:
![]()
![]()
![]()
Thus in order to have a concentration of 0.20 mg.L-1 Mn in the solution, we need to add 0.811 g of ![]() in 1,000 litre of water.
in 1,000 litre of water.
Now we will calculate the Boron (B) requirement
We will use ![]() to provide Boron which has 17.80 % B.
to provide Boron which has 17.80 % B.
According to the water analysis there is 0.1 mg.L-1 B in the irrigation water so the amount of B required from fertilizers is 0.4 mg.L-1. The amount of Boric acid to add in the irrigation water (in a 1,000 L tank) will be:
![]()
![]()
![]()
Thus in order to have a concentration of 0.50 mg.L-1 B in the solution, we need to add 2.25 g of ![]() in 1,000 litre of water.
in 1,000 litre of water.
We will now solve the Cupper (Cu) requirements
We will use Copper sulphate ![]() which has 25.63 % Cu content.
which has 25.63 % Cu content.
According to the water analysis there is no Cu in the irrigation water so the amount of Cu required from fertilizers is 0.05 mg.L-1. The amount of Copper sulphate to add in the irrigation water (in a 1,000 L tank) will be:
![]()
![]()
![]()
Thus in order to have a concentration of 0.05 mg.L-1 Cu in the solution, we need to add 0.20 g of ![Rendered by QuickLaTeX.com in 1,000 litre of water. We will now calculate the molybdenum requirements. Ammonium molybdate [latex]\ce{(NH4)6Mo7O24.4H2O}](https://www.commercial-hydroponic-farming.com/wp-content/ql-cache/quicklatex.com-d3242287a88ecc19c9c3e1357e3e2265_l3.png) with 57.73 % Mo will be used.
with 57.73 % Mo will be used.
According to the water analysis there is no Mo in the irrigation water so the amount of Mo required from fertilizers is 0.5 mg.L-1. The amount of Ammonium molybdate to add in the irrigation water (in a 1,000 L tank) will be:
![]()
![]()
![]()
Thus in order to have a concentration of 0.50 mg.L-1 Mo in the solution, we need to add 0.87 g of ![]() in 1,000 litre of water.
in 1,000 litre of water.
Now calculate the Zink (Zn) requirments.
According to the water analysis there is 0.02 mg.L-1 Zn in the irrigation water so the amount of Zn required from fertilizers is 0.03 mg.L-1. The amount of NaZnEDTA to add in the irrigation water (in a 1,000 L tank) will be:
![]()
![]()
![]()
Thus in order to have a concentration of 0.05 mg.L-1 Zn in the solution, we need to add 0.2 g of NaZnEDTA in 1,000 litre of water. Like Fe, Zn availability to plants is pH dependant. If the pH is high, Zn will precipitate as insoluble ![]() . Zn is also adsorbed onto carbonates if there is high carbonate in the water with high Ca level. Compensating for water Zn should be done with great care since the water Zn might not be available due to above factors. Ensure that the pH is below 6.5 for optimum Zn uptake. If there is high carbonate concentration, the water Zn should be ignored and the full 0.05 mg.L-1 must be added in NaZnEDTA form.
. Zn is also adsorbed onto carbonates if there is high carbonate in the water with high Ca level. Compensating for water Zn should be done with great care since the water Zn might not be available due to above factors. Ensure that the pH is below 6.5 for optimum Zn uptake. If there is high carbonate concentration, the water Zn should be ignored and the full 0.05 mg.L-1 must be added in NaZnEDTA form.
The total amount of fertilizers added to supply micro nutrients are listed below. As can be seen from the table each fertilizer supplies only one element in comparison with the macro fertilizers where each fertilizer contains at least two nutrients. The amounts are also much smaller than with the macro elements. If mixing small volumes such as 1,000 L, it would be easier to by pre-mixed micro nutrients from a fertilizer company. The reason is that weighing 0.2 g requires special equipment which is very expensive. If however larger amounts are mixed, using either 10,000 L tanks or mixing stock solutions (as explained in the next section), the amounts are easier to measure and measurement errors will be insignificant.
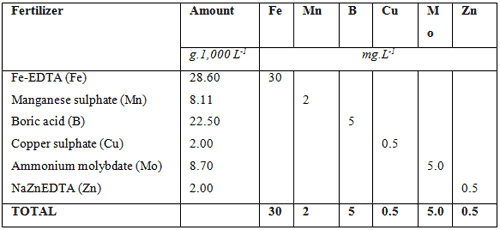
In above examples a 1,000 L nutrient tank is used to mix the fertilizers. In a small home hydroponic system this would be adequate but for commercial systems a 1,000 L tank would be hopelessly to small. The minimum size for a bag culture system would be 10,000 L, which would be used for 5,000 m² hydroponic farm. The amount of fertilizers required to supply the macro nutrient as provided in the ‘sample requirement table’, are listed in table below and the total amount of fertilizers needed to supply the micro nutrients are listed in the table thereafter if a 10,000 L tank is used. As can be seen, the amounts are 10 times more than in a 1,000 L tank and they are easier to measure. A 1 g mistake, for instance for Fe chelate from 3.0 g would mean either 2g or 4 g being measure, but for a 10,000 L tank it would mean either 29 g or 31 g being measured. The difference in the small tank is either 33 % over or under measuring or in the case of the large tank a 3.3 % mistake being either over or under.
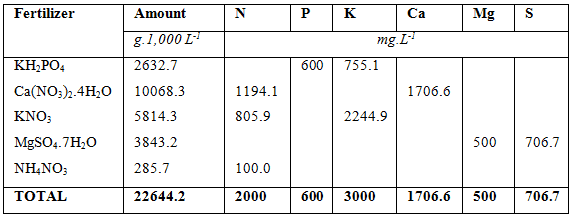
Total amount of fertilizers used to solve the hypothetical macro-nutrient solution (10,000 L tank used).
Share This Story, Choose Your Platform!
Cotton aphid – Aphis gossypii
Cotton Aphid, or Aphis gossypii, is one of the more common insect pests found in almost all vegetable crops and [...]
Greenhouse white fly
Description Greenhouse white fly, also known as Trialeurodes vaporariorum is a sap feeder. The easiest way to find white flies [...]